infinite michelson ?
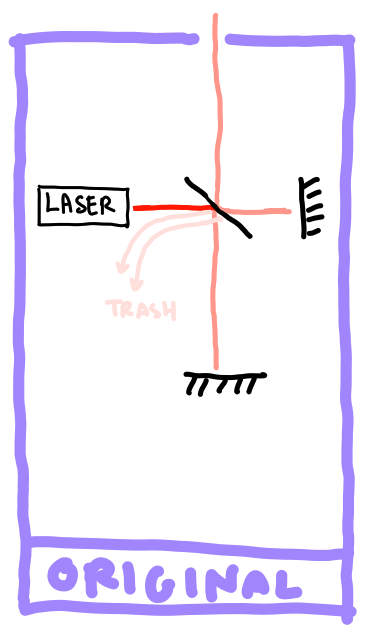
Here is the original setup : a laser beam is splitted by a beam splitter. Half of the signal goes through a path on a certain length, and the other half through an other path of different length. The combined beam will, depending on the difference between the two paths, eventually cancel out.
There are a few different beam splitters with different behaviors... It could affect the following steps, but I guess this is still interesting. I will for now ignore this and assume a beam splitters that behaves as I wish : half goes through, half is reflected, there is no internal state that would influence the next splitter's outcome.
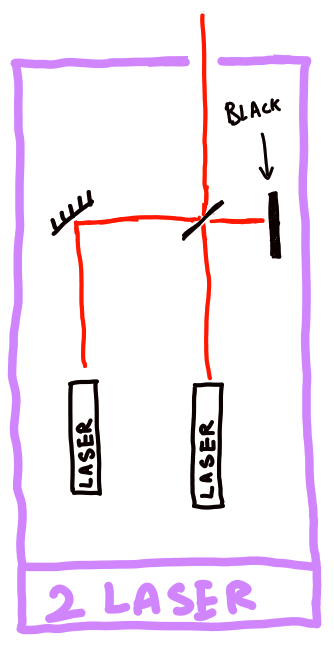
Now let's make a modification to the original setup : we bring in two identical lasers and make them interfer, let's call that thing a $2$-laser.
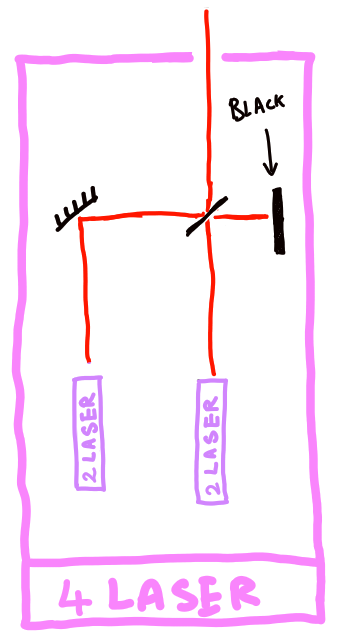
This whole thing can be seen as a single beam generator. So we replicate this pattern and use itself to make a $4$-laser. Obviously, we are going to continue recursively to make a $2^n$-laser.
Great, now let's make a huge $2^n$-laser (we could also make any number by combining $2^n$ with $2^m$ lasers, basically writing down a number in binary... but note that given the signal is weaken by the beam-splitter's loss into the black spot, we better keep the full structure of a single $2^n$-laser and shut some individual lasers down, so that the contribution per laser to the final signal doesn't change.)
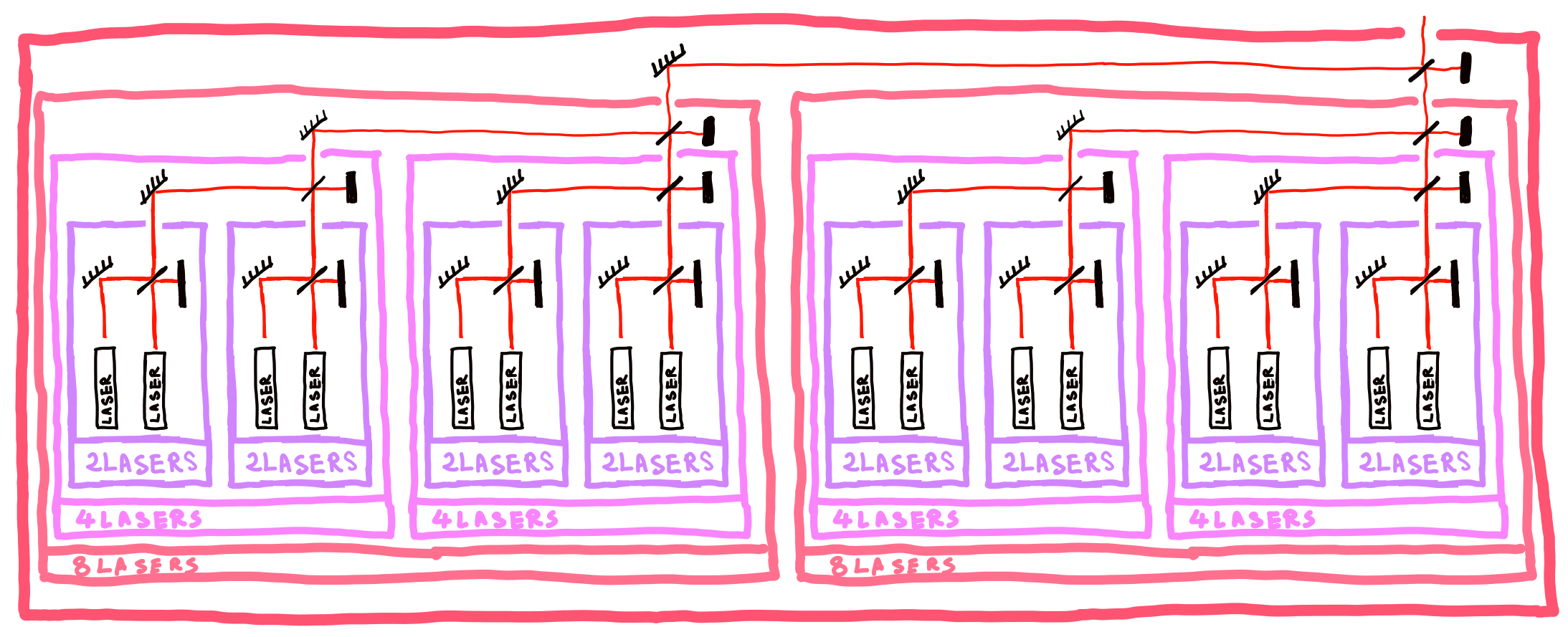
What is the signal on average for $n$ huge ?
Let's look at the output of the $j^{th}$ laser as an oscillation of the electrif field (ignoring polarization)
$$ s_j(z) = E⋅a(z)⋅\exp(iω(t-z/c)+φ_j)$$
where
$z$ the distance along the laser's path starting from the laser,
$E$ the strength of the oscillation at $z=0$,
$c$ is the speed of light,
$ω$ the pulsation of the laser,
$φ_j$ a phase associated to the specific laser,
$a(z)$ the attenuation the beam got because of the beam-splitters.
We tune every laser such that if we only switch on one laser at a time (in our $2^n$ setup), the output $E$ excitation will be of stregth $1$ (we compensate for all beam-splitting losses). This convention depends on the choice of $n$.
In this configuration, by switching all lasers on, we get a final signal that is $$ s = ∑_j \exp(iωt+ϕ_j)$$ where $ϕ_j$ contains the phase shift of the laser ($φ_j$) and the phase shift due to space travel ($-iωz/c$). These $ϕ_j$ are some constants that are the result of an uniform random variable in $[0,2π]$ (nothing is tuned in our setup, therefore no phase has a higher probability to occur).
We can rewrite $$ s = ∑_j \exp(iωt)\exp(ϕ_j) = \exp(iωt) ∑_j \exp(ϕ_j) $$
$\exp(iωt)$ is shared across all realization. The amplitude contribution is a factor of $1$, the oscillation speed indicates the color of the output beam.
This means $∑_j \exp(ϕ_j)$ fully define the final phase and amplitude.
When considering an infinite sum like this, my intuition says that given that the probability of getting phase $ϕ$ equals the probability for $-ϕ$, I expect the sinal to converge to $0$, which is super weird : the more (normalized, given the beam-splitter setup) lasers, the weaker the signal ?!?
This is misleading.
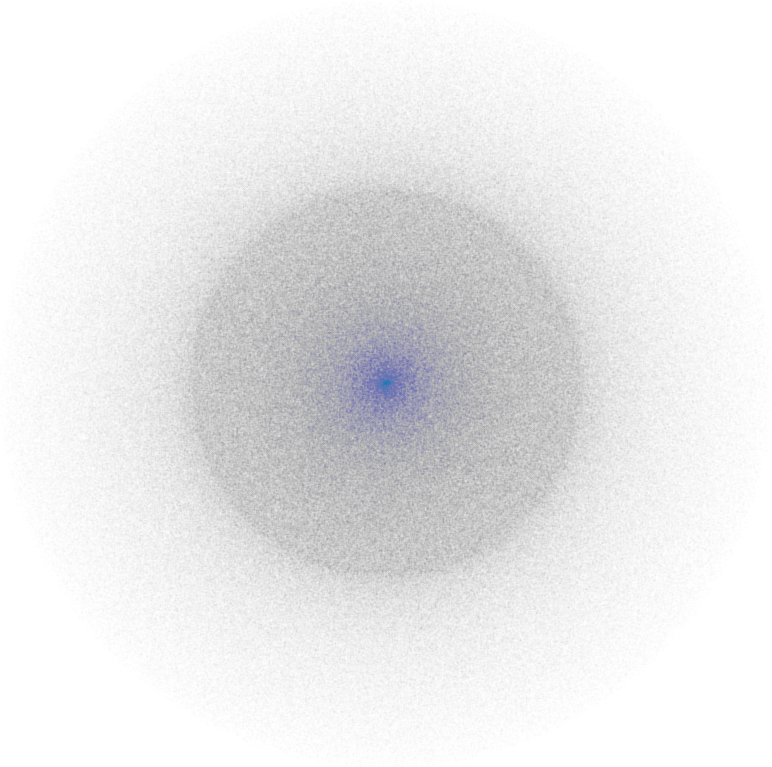
$∑_j \exp(ϕ_j)$ can be seen as a random walk on the complex plane. At each step we choose an angle, and move $1$ step in that direction. We repeat the process. So the distribution of the final position of the walk is given by a succession of $k$ convolutions of the unit circle, where $k$ is the length of the walk.
Let's look at the distribution at different steps.


 ...
...

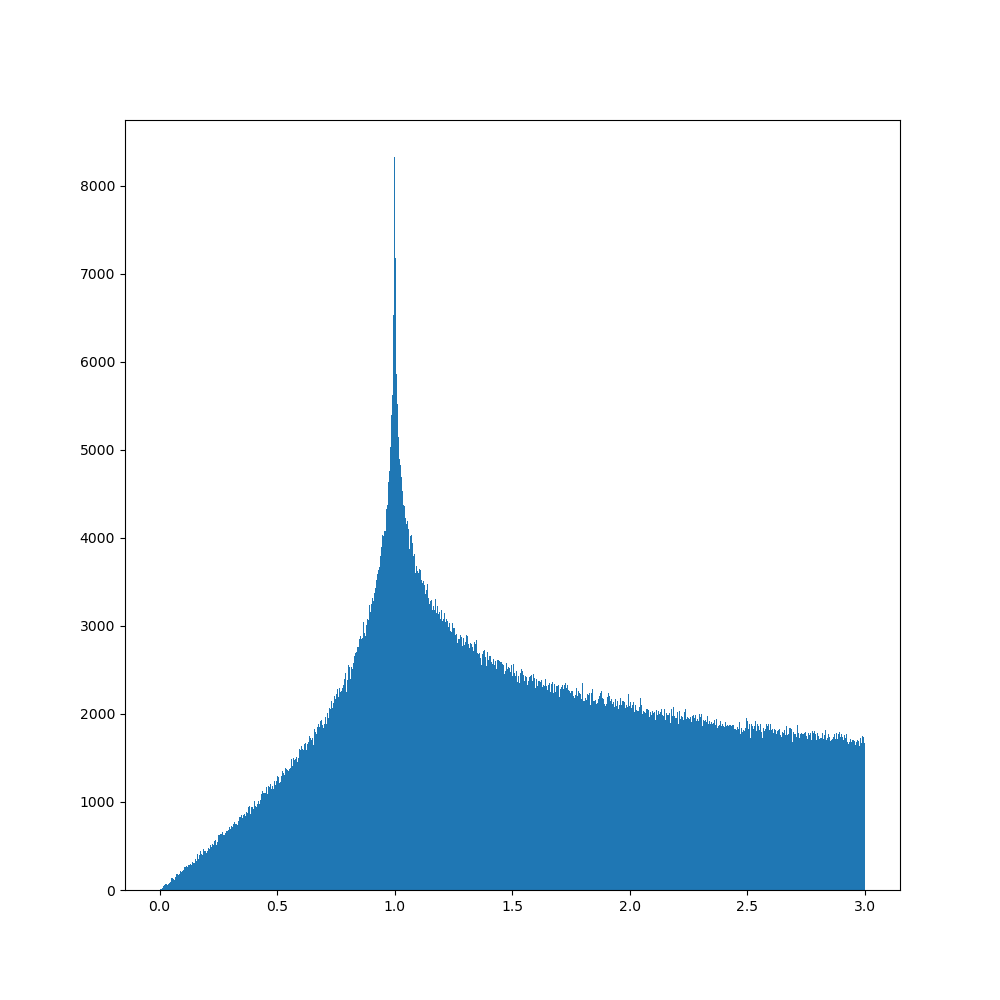
 $1$ step walk
$1$ step walk(radius $1$) $2$ steps walk
(radius $2$) $3$ steps walk
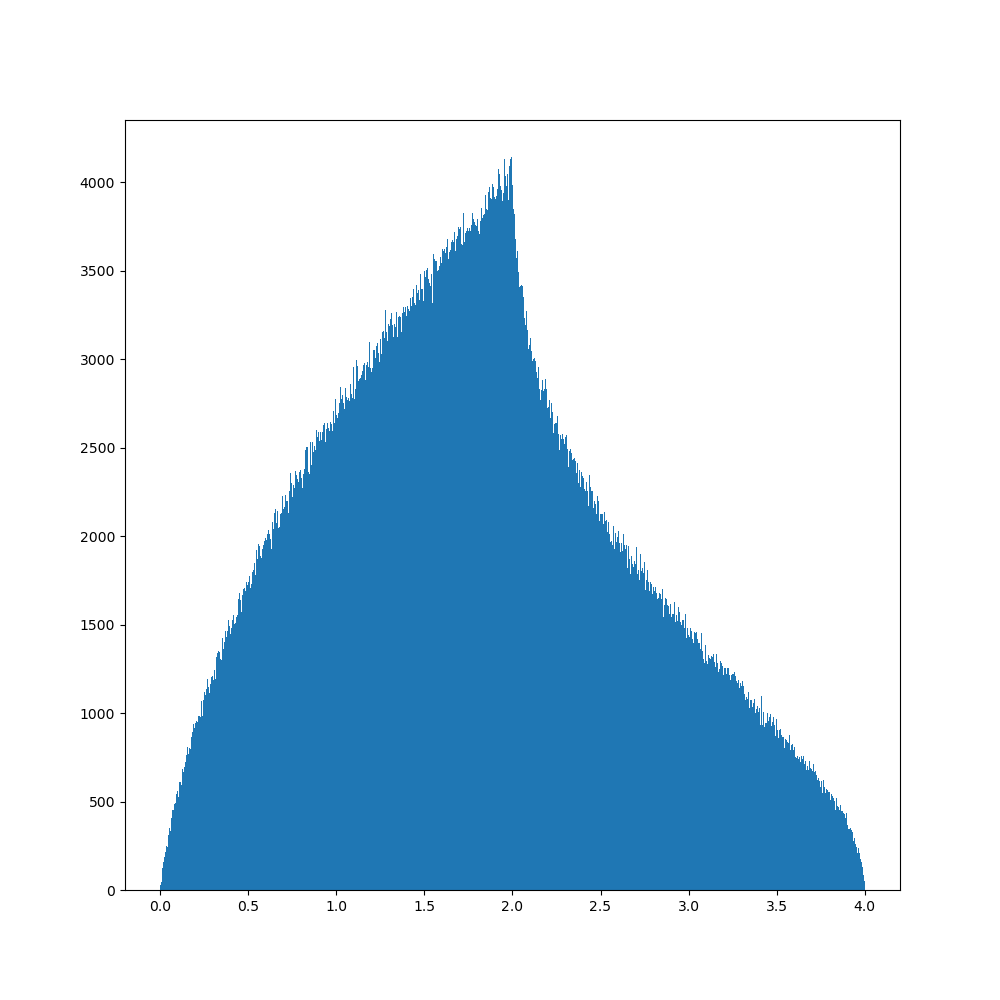
(radius $3$) $4$ steps walk
(radius $\sim4$) ... $100$ steps walk
(radius $\sim 30$) $1000$ steps walk
(radius $\sim 100$)
Here is a funny thing : let's look at the $2$ steps walk. If you look at any point :
- either there is no way to get there in $2$ steps (outside the circle of radius $2$)
- or there is only $2$ ways to get there (inside the circle of radius $2$)
- or there is only $1$ way to get there (border of the circle of radius $2$)
- or there is $∞$ ways to get there (center of circle of radius $2$)
With this description, it looks like we should have an uniform distribution inside the circle (except border and center), but we don't. It's kind of hilarious when you think about it : the density in a small patch will vary, but for any points it's always the same thing : there are only $2$ ways to get there.
Let's now collapse radially because the strengh of the signal doesn't depend on the phase.
 ...
...
 $1$ step walk
$2$ steps walk
$3$ steps walk
$4$ steps walk
...
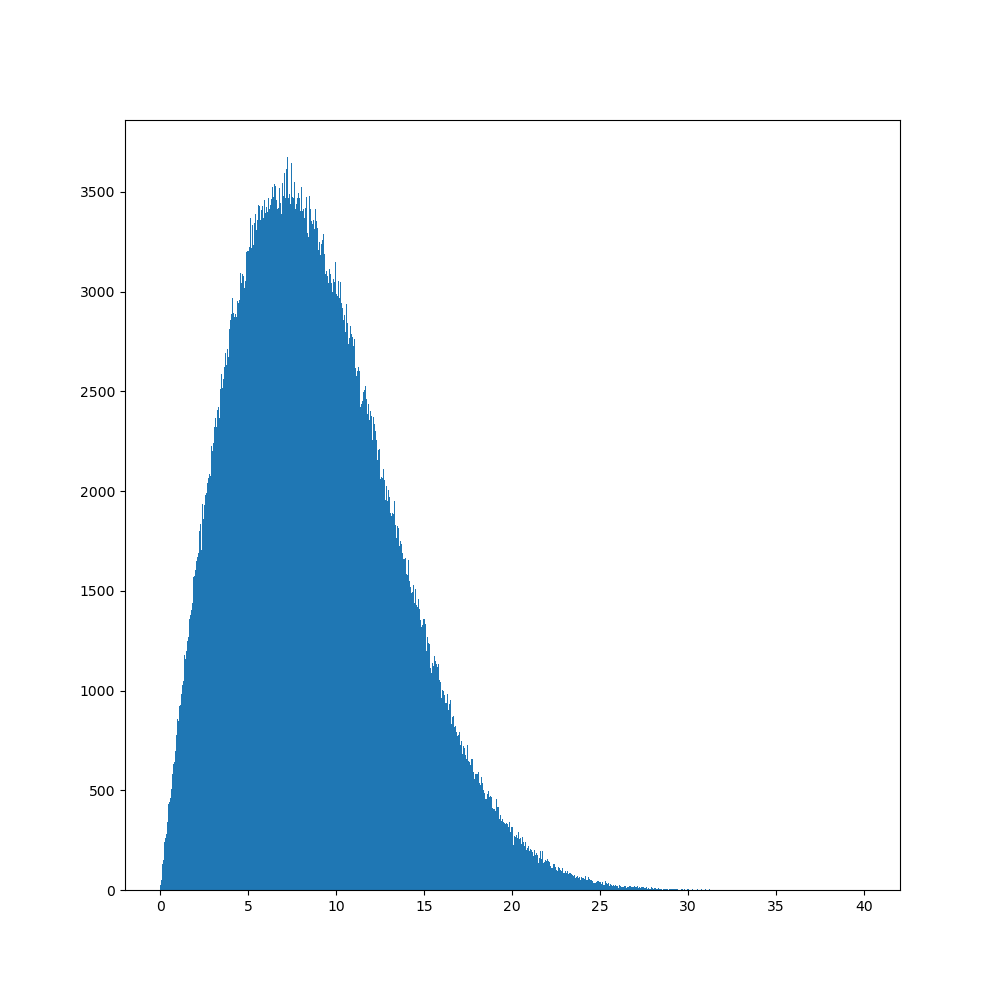
$100$ steps walk
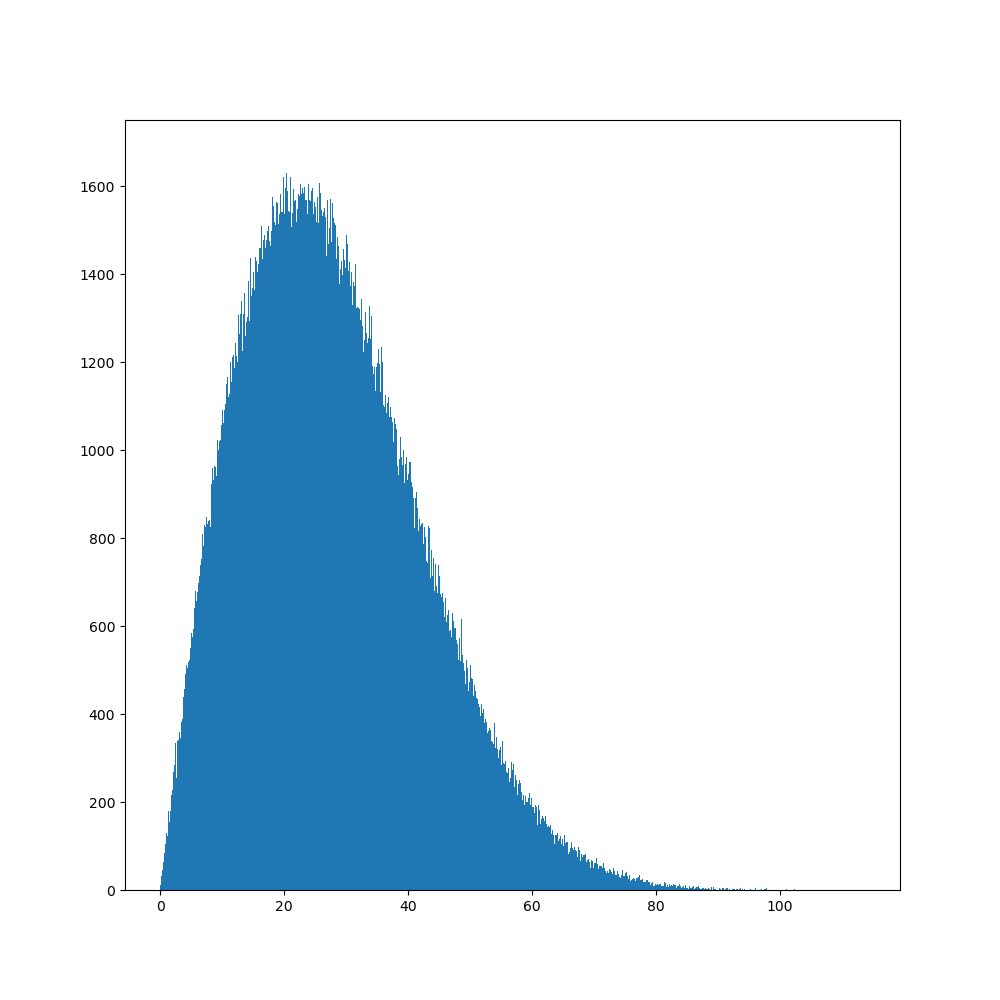
$1000$ steps walk
$1$ step walk
$2$ steps walk
$3$ steps walk
$4$ steps walk
...
$100$ steps walk
$1000$ steps walk
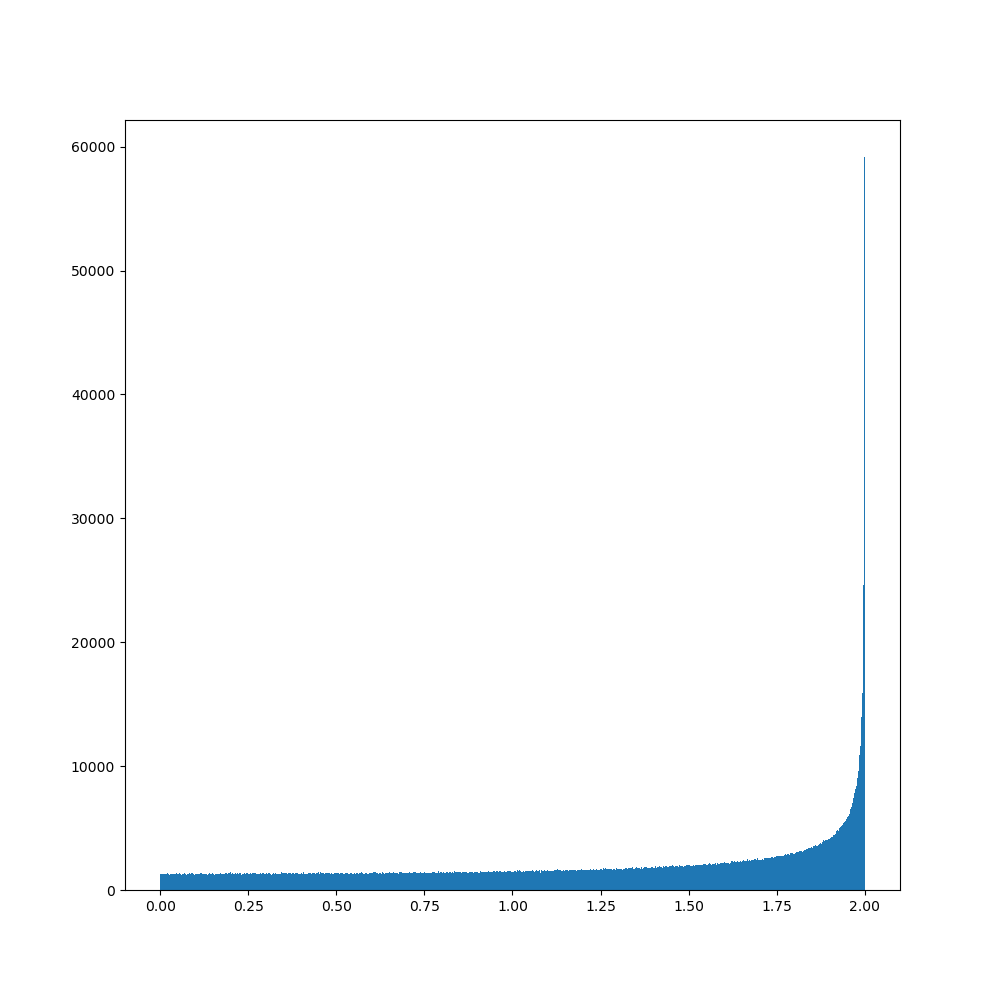
The population around $0$ gets much smaller. This is because when collapsing a circle, we collect a population that was spread along a curve of length $2πr$, so for $r$ small, the total population ends up being small.
We can see here that even though there is a good chance to cancel our progression, the population slowly gets farther from $0$, and there seem to be no limit to that growth with iterations. Also chance to be very close to $0$ weakens.
However, if we didn't normalize our laser (thus kept total ouput maximum $E$ strength to $1$), then we would have seen a vanish.
This part tricked me when I first ran a quick numerical test because summation and average behave in very different manners here.